Explanation:
Since these values are supplied, start by calculating the total cost of the onions and carrots. This equals ($20.25) x (2 x $3.69) x (3 x $4.29). The cost of the mushrooms is then calculated by subtracting this amount from the total cost of the vegetables: $24.15 - $20.25 = $3.90. Finally, the cost per pound is calculated by dividing the cost of the mushrooms by the quantity (lbs):
$3.90/1.5 = $2.60 per pound
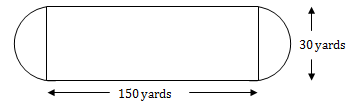
Explanation:
First, add the two 150-yard straight sections. Also, the circumference of a circle is formed by the distance between the two semi-circular turns. The radius (r) of that circle is 15 yards or half of the dimension displayed as the track width. Taking the formula for a circle's circumference, 2πr, and multiplying it by the length of the two straight sections of the track, we get
Length = (2π × 15) + (2 × 150) = 394.25.
The closest approximation to this computed result is 395 yards.
Explanation:
This problem can be solved in one of two ways: convert meters to centimeters and then use the conversion factor in the table to convert centimeters to inches, or convert meters to yards and then convert to inches using the table.
To begin, remember that a meter is made up of 100 centimeters (centi meaning "hundredth"). As a result, 19m = 1900cm = 748 inches (1900/2.4).
In the second case, remember that a yard is 36 inches long; therefore, 19 m 1.094 yd/m = 20.786 yd 36 in/yd = 748 in.
Conversions are frequently made using proportions. Set up proportions to solve for an unknown variable, x. (1900 cm)/(x in)=(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/(2.54 cm)/( (1 in)
To solve for x, multiply 1900 by 2.54 to get 1900 = 2.54x, then divide each side by 2.54 to get 748.
Explanation:
Candidate A's vote percentage is calculated by dividing the number of votes he received by the total number of votes cast. Then, to convert the decimal to a percentage, multiply it by 100. As a result, Candidate A's vote is as follows:
Percentage 36800/(36800 + 32100 + 2100) ×100 = 51.80%
Explanation:
Because 16 seats are unfilled, accounting for 2/5 of the total enrolment, the whole class must be made up of
Class = 5/2 × 16 = 40 students
Use proportions
2/5 = 16/x
Cross multiply to get: 2x = 80, then divide each side by 2 to solve for x. x = 40 students
Explanation:
The sum of the numbers in a data set divided by the total number of items is the mean, or average. There are seven entries in this data set, one for each day of the week. Kyla had a total of 14 hits during the week, which is the sum of the figures in the right-hand column.
This gives: Mean = 14/7 = 2.
Explanation:
The rate of increase is calculated by dividing the change in the account balance by the starting amount, which is $80. To get the percentage increase, multiply the decimal by 100. Subtract the initial amount from the new balance to find the balance change: $120 minus $80 equals $40.
Now, as indicated previously, calculate the percentage increase:
Percentage = $40/$80; 100 percent = 50%.
Advertisement
Explanation:
To calculate David's profit per share, divide his total profit of $22.00 by the number of shares he purchased, 200:
P = $22.00 ÷ 200 = $0.11, or 11 cents per share As a result, the price he paid was 11 percent less than the closing price in the table. Because Oracle ended at $19.11 per share today, David paid $19.11 - $0.11 = $19.00 per share,
Explanation:
Since there are four different colors, one color must be excluded from each balloon bundle. Therefore, there is one color set for each excluded color, or four in all.
This problem can also be solved mathematically as follows. An arrangement such as this, in which the order of the individual components is not important, is called a combination. The number of combinations of n objects taken k at a time is given by = 2!/((n − k)!k!) . The ! notation indicates a factorial product, where n! = 1 × 2 × 3 × ... × (n − 1) × n. In this case, n = 4 colors, and k = 3 balloons per bundle. Substituting into the equation above, and simplifying: C = 4!/((4 − 3)!×3!) = (1 × 2 × 3 × 4)/((1)(1 × 2 × 3)) = 4
Explanation:
When the height is set to Y, the volume is calculated as the product of the length, width, and height: 6 x 7 x Y = 378. 378 / 42 = Y = 9 can be rearranged in this way.
Explanation:
There are three times as many females as boys in the class, it is 75 percent girls and 25% boys. We solve the following equation to obtain the average amount of points each boy receives: 0.75*18 + 0.25*X = 17, where X is the average number of points scored by each boy. When you solve for X, you get X = 14, which means the boys score 14 points every game on average.
Explanation:
The base wage for Johnny is calculated by multiplying his hourly wage by the number of hours he worked: $8.50 x 36 = 306.
His oil-change bonus is computed by multiplying the payout per oil change by the number of oil changes completed:
17 multiplied by three equals 51. After then, the two goods can be combined.
Explanation:
There are 48 possible tie and shirt combinations (eight ties for each of the six pairs of pants) and four different shirts for each of these pairings. 8 x 6 x 4 = 192 in numerical representation.
Explanation:
To calculate the price of 3 inches of rope, multiply the number of inches in 2 feet (24) by 3 and multiply this amount (8) by the price of 3 inches of rope:
8 x 7 = 56.
Advertisement
Explanation:
This type of problem can be readily handled by taking the average of the two range extremes:
(13 + 37) / 2 = 25.
Explanation:
Make sure you know where the decimal point is.
Explanation:
By using the oil, Arman will save just $10 (.5 x (500 / 25)), which is still $6 less than the cost of the oil.
Explanation:
Rather than looking at the value of the first digit in the number, make a note of the number of place values.