PARCC High School Algebra 1 Practice Test Questions

FREE PARCC High School Algebra 1 2026 practice tests. Get our 545+ questions and answers online to help you pass your exam. [Updated March 2026]

PARCC - Partnership for Assessment of Readiness for College and CareersBy Dr. Lisa PatelApr 2, 20266 min read

1. Fill in the blanks to complete the following sentence. The graph of the equation y=2(x+3)-4x+(x-3)(x+1) is a ________ with zeros at _ and __ and a minimum at y=_. (Ambien)

Correct! Wrong!

1. Parabola, 3, 1, -1: y=2(x+3)-4x+(x-3)(x+1) simplifies to y=x^2-4x+3, and the zeros of the graph of the equation occur when y=0. To solve 0=x2-4x+3, use the factored form 0=(x-3)(x-1) and set each factor equal to zero. Then, solve for x: (x-3)(x-1)=0 (x-3)=0 (x-1)=0 x=3 x=1 The graph of the quadratic equation ax^2+bx+c is a parabola with an axis of symmetry x=-b/2a, and the maximum or minimum value of a parabola lies on the axis of symmetry. Find the equation which represents the axis of symmetry, and find the y-value for the determined value of x: For =x2-4x+3, a=1,b=-4,c=3. The axis of symmetry is x= (-(-4))/2(1) =2. When x=2, y=(2)2-4(2)+3=4-8+3=-1.

2. Part A: If there exists a linear relationship between the input and output values, which, if any, of these input/output pairs can be included in the data set? Choose all that apply.

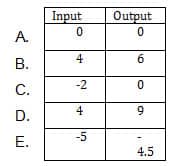
Correct! Wrong!

2. C, D, E; y=3/2 x+3: The rate of change in a linear relationship is constant. In the given table, the output, or y, value decreases by three as the input, or x, value decreases by 2. The slope m of the line between the two given points is, therefore, (-3)/(-2)=3/2. A linear equation can be written in slope-intercept form, y=mx+b. Substitute one of the given x-y pairs and the determined slope into the equation to find the y-intercept b: y=mx+b 3=3/2(0)+b 3=b Using the determined slope and y-intercept, the equation of the line in slope-intercept form is y=3/2 x+3. Using this equation, input values x=0,4,-2,-5 gives output values y=3,9,0,-4.5, respectively. Of the answer choices, (-2,0),(4,9), and (-5,-4.5) lie on the same line the one which passes through given points (2,6) and (0,3).

3. The solution to which of the following systems of inequalities is graphed below?

A. y<-3x+4
4x-2y<6

B. y > 2x-3
y<3x+4

C. x<-3y+4
y+3 < 2x

D. y>4-3x
y > 2x-3

E. None of the above

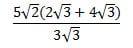
Correct! Wrong!

4. Simplify the expression.

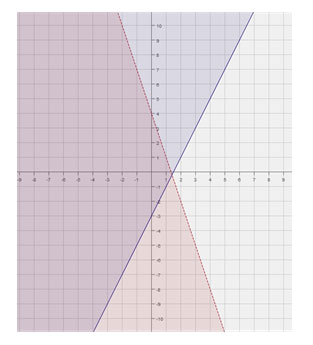
Correct! Wrong!

5. Write a piece-wise function to describe the graph below.

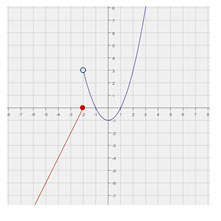
Correct! Wrong!

The graph as x approaches -2 from the left is linear; the slope of the line is 2, and, if the line were extended, it would cross the y-axis at 4. Therefore, in slope-intercept form, the equation of the line is y=2x+4. The function is defined by this line for all x-values less than or equal to -2. Once x exceeds -2, the graph is a parabola. This parabola is the graph of y=x2 shifted down one unit, so its equation is y=x2-1.

Candidates can also sharpen their skills with our PARCC practice test 2026, which includes hundreds of practice questions in the exact format and difficulty of the real exam.

Students and adults undergoing academic evaluation can review with our WRAT Wide Range Achievement Test practice — covering word reading, sentence comprehension, spelling, and math computation.

Arkansas students can prepare for ACT Aspire and state benchmark exams with our free Arkansas state assessment practice test — covering ELA, mathematics, and science at grade-level standards.

PARCC Practice Test Questions

Prepare for the PARCC - Partnership for Assessment of Readiness for College and Careers exam with our free practice test modules. Each quiz covers key topics to help you pass on your first try.

PARCC Advanced Grammar Practice Questions

PARCC Exam Questions covering Advanced Grammar Practice Questions. Master PARCC Test concepts for certification prep.

PARCC High School Algebra 1 Practice Test Questions

1. Fill in the blanks to complete the following sentence. The graph of the equation y=2(x+3)-4x+(x-3)(x+1) is a __________ with zeros at ___ and ____ and a minimum at y=___. (Ambien)

2. Part A: If there exists a linear relationship between the input and output values, which, if any, of these input/output pairs can be included in the data set? Choose all that apply.

3. The solution to which of the following systems of inequalities is graphed below?

4. Simplify the expression.

5. Write a piece-wise function to describe the graph below.

PARCC Practice Test Questions

PARCC Advanced Grammar Practice Questions

PARCC Advanced Mathematics Practice Questions

PARCC Advanced Reading Practice Questions ...

PARCC Algebra Practice Test

PARCC Author's Purpose Practice Questions ...

PARCC Averages and Rounding Practice Quest...

PARCC Basic Operations Practice Questions

PARCC Comma Practice Test Questions

PARCC Estimation Sequence Practice Test

PARCC Exponent Practice Problems - Test

PARCC Fractions and Square Root Practice Q...

PARCC Geometry Practice Test

PARCC Grade 3 ELA Practice Test Questions

PARCC Grade 3 Math Practice Test Questions

PARCC Grade 4 ELA Practice Test Questions

PARCC Grade 4 Math Practice Test Questions

PARCC Grade 5 ELA Practice Test Questions

PARCC Grade 5 Math Practice Test Questions

PARCC Grade 6 ELA Practice Test Questions

PARCC Grade 6 Math Practice Test Questions

PARCC Grade 7 ELA Practice Test Questions

PARCC Grade 7 Math Practice Test Questions

PARCC Grade 8 ELA Practice Test Questions

PARCC Grade 8 Math Practice Test Questions

PARCC Grade 9 ELA Practice Test Questions

PARCC Grammar Practice Online Questions

PARCC Grammar Practice Questions

PARCC Graph Practice Questions - Test

PARCC Intermediate Mathematics Practice Qu...

PARCC Mathematics Practice Questions

PARCC Measurement Practice Problems

PARCC Noun Practice Quiz

PARCC Percent and Ratio Practice Questions

PARCC Reading Comprehension Practice Test ...

PARCC Reading Main Idea Practice Questions...

PARCC Reading Vocabulary Practice Questions

PARCC Sentence Correction Practice Questions

PARCC Sentence Flow Practice Questions

PARCC Usage Practice Questions

PARCC Verb Practice Test Questions

PARCC Word Usage Practice Test Questions

PARCC Writing Practice

PARCC Writing Practice Questions

1. Fill in the blanks to complete the following sentence. The graph of the equation y=2(x+3)-4x+(x-3)(x+1) is a ________ with zeros at _ and __ and a minimum at y=_. (Ambien)