SBAC High School Math 2 Practice Test
The polynomial, x^3+7x^2-20x-96, has a factor of (x+8). Which of the following represents two of the zeros of the polynomial?
Since the polynomial has a factor of x+8, synthetic division of the given polynomial by −8 may be completed. Recall the factor is in the form, (x-a); equals , so a=-8. Synthetic division reveals x^3+7x^2-20x-96=(x+8)(x^2-x-12).The factor x^2-x-12, which can be further factored as (x+3)(x-4). Setting each factor equal to zero gives x=-3 and x=4. Thus, two more zeros of the polynomial are x=-3 and x=4. The zero that may be directly determined from the problem is x=-8.
The possible combinations of candy bars and packages of suckers that Amanda may purchase are represented by the graph shown below.
Which of the following inequalities represents the possible combinations of candy bars and packages of suckers that she may purchase?
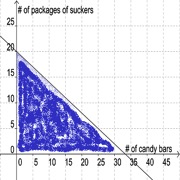
The y-intercept of the inequality is 20, and the slope is −0.6. The slope can be determined by calculating the ratio of the change in y-values per change in corresponding x-values. Using the y-intercept and the point, (25, 5), the slope can be written as (5-20)/(25-0), which equals −0.6. Since the evaluation of the inequality for x- and y-values at the origin produces a true statement, the side of the plane containing the point, (0, 0) should be shaded. The inequality, 0.75x+1.25y≤25, solved for y, may be written as y≤-0.6x+20.
Ana solves the quadratic equation, x^2-6x=18, by completing the square. Which of the following equations may be used to find the solution, using this method?
When completing the square, the coefficient of the x-term, or −6, should be divided by 2 and then squared. Doing so gives 9. This constant should be added to both sides of the equation. Thus, the equation may be written as x^2-6x+9=27. The left side of the equation may be written as 〖(x-3)〗^2. Thus, the equation that may be used to find the solution of the equation, using the method of completing the square, is 〖(x-3)〗^2=27.