SBAC Grade 6 Math Practice Test
Daniella wrote a decimal and a fraction which were equivalent to each other. Which pair of numbers could be the pair Daniella wrote?
To answer this question, one method that can be used is to convert all the fractions to decimal form so it is easier to compare them to each other. This can be done by simply dividing, since the fraction sign means division. 7÷8=0.875 3÷8=0.375 7÷5=1.4 4÷5=0.8 So, the only pair of numbers in which the fraction is equivalent to the decimal is in answer B.
One morning at Jim's café, 25 people ordered juice, 10 ordered milk, and 50 ordered coffee with breakfast. Which ratio best compares the number of people who ordered milk to the number of people who ordered juice?
Note that the ratio asked for is the number of people who ordered milk to the number who ordered juice. The number of people who ordered coffee does not matter here. This compares 10 to 25, and the order is important here. Since the ratio is with the number of people who ordered milk first, the 10 must come first. So, the ratio is 10 to 25, but the ratio can be written in simpler form by dividing both numbers in the ratio by 5, to get the ratio: 2 to 5
A unit of liquid measure in the English System of Measure is the gill. The table, shown here, gives conversions from gills to fluid ounces.
Which equation best describes the relationship between gills, g, and fluid ounces, f?
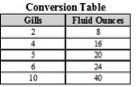
Looking at the chart, a pattern can be seen in the relationship between the number of gills and the number of fluid ounces. Each number of gills in the first column, when multiplied by 4, gives the number of fluid ounces in the second column. So, f equals 4 times g, or f = 4g.
The table below shows changes in the area of several trapezoids as the lengths of the bases, b1 and b2, remain the same and the height, h, changes.
Which formula best represents the relationship between A, the areas of these trapezoids, and h, their heights?
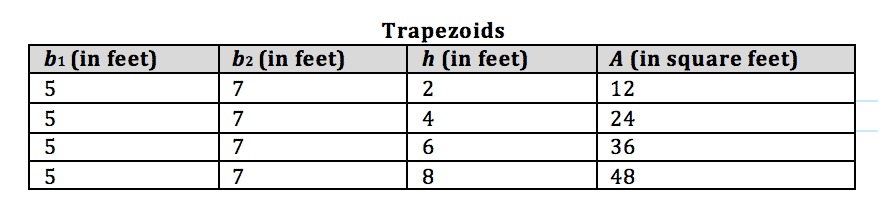
The formula for the area of trapezoids is not necessarily needed here to do this problem. Since the relationship between the area, A, and the height, h, can be seen in the chart, looking at the third and fourth columns to see if there is a pattern will show a relationship between the variables. Each value in the area column is equal to 6 times the value in the height column. So, we get A=6h.
Ellen measured ∠R in the parallelogram shown here and found it to be 35°. She knows that ∠R and ∠T have equal measures. She also knows ∠S and ∠V are equal in measure.
What is the measure of ∠V?

The angles opposite each other in a parallelogram are equal in measure. So, ∠R has an equal measure to ∠T, or 35°. The sum of the measures of these two angles is 35 + 35 = 70. The sum of the measures of all four angles of a quadrilateral is 360°. We subtract 360 – 70 to get 290. So, 290° is the sum of the measures of the other two equal angles, ∠S and ∠V. Then we divide 290 by 2 to get 145. We know that ∠V has a measure of 145°.