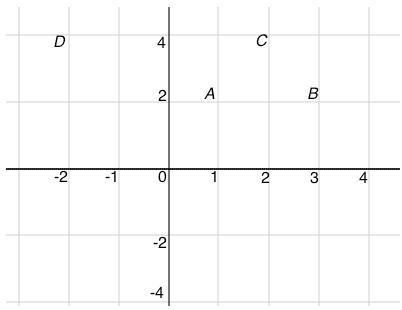
The coordinates of A are (1,2), the coordinates of B are (3,2). The slope of AB is (2-2)/( 3-1) = 0 The coordinates of A are (1,2), the coordinates of D are (-2,4). The slope of AD is (4-2)/( -2-1) = -4/3 The coordinates of A are (1,2), the coordinates of C are (2,4). The slope of AB is (4-2)/( 2-1) = 2 The coordinates of D are (-2,4), the coordinates of B are (3,2). The slope of DB is (2-4)/( 3− -2) = -4/5
If B is reflected in the x-axis its x-coordinate will not change but it will be as far below the x-axis as it currently is above the x-axis. Its coordinates, after reflection, will be (3, -2)
(24 x 32) / (2 x 3)= 24-1 × 32-1. 24-1 × 32-1 = 23 × 31 23 × 31 = 23 × 3
The platform is reached when h = 0. It is necessary to solve the equation 0 =-t2+3t+10. This can be rearranged to t2-3t-10 = 0. Hence (t - 5)( t + 2) = 0. Solving the equation gives t = 5 or -2. As t is a time it is not possible for t to be -2. The rocket takes 5 seconds to reach the platform.
10x2 - 11x + 3 = 10x2 - 5x - 6x + 3 10x2 - 5x - 6x + 3 = 5x(2x - 1) - 3(2x - 1) 5x(2x - 1) - 3(2x - 1) = (5x - 3)(2x -1)
3.25 feet = 1 meter 1 foot = 1÷3.25 meters 21 feet = 21×1÷3.25 = 6.4615 meters
y =15 - 3x and y = 0 Hence 15 - 3x = 0 Hence 3x = 15 x = 5
10 people can paint a building in 5 days. Each person paints 1/10 of the building in 5 days. In 5 days 7 people would paint 7 × 1/10 of the building In 5 days 7 people would paint 7/10 of the building.
The distance between numbers can be found by using absolute values (|a| or abs(a)). The distance between these numbers is abs(-3/7 − -2/3 ) = abs(-(3/7 -2/3)) = abs(3/7 -2/3) = abs(9/21 - 14/21) = abs(-5/21 ) =5/21
If 1/4, 2/3, 4/7, 1/2 are converted to decimals we get 0.25, 0.6666...., 0.571....., 0.5 then the correct order is obvious or If 1/4, 2/3, 4/7, 1/2 are converted to fractions with a common denominator 21/84, 56/84, 48/84, 42/84 then the correct order is obvious.