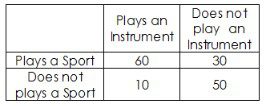
From the table, we see that 30 students play an instrument but do not play a sport.
Now, we can find the fraction of students who play an instrument but do not play a sport:
Fraction = 30 ÷ 90 = 1/3
However, since we need the total number of students surveyed to calculate the fraction of those who play an instrument but do not play a sport relative to the total number of students (150):
Fraction = 30 ÷ 150 = 1/5
The correct answer for the fraction of students who play an instrument but do not play a sport is 1/5.
So, the total number of students who play a sport is:
Total who play a sport = Students who play both + Students who only play a sport = 60 + 10 = 70
Now, we know there were 150 students surveyed in total. Therefore, the fraction of students who play a sport is:
Fraction = Number of students who play a sport ÷ Total number of surveyed students = 1/5
Fraction = 70 ÷ 150 = 7/15
The correct answer for the fraction of students who play a sport is 7/15.
An integer is a whole number that can be positive, negative, or zero, but it cannot be a fraction or a decimal.
To rotate a point (x, y) 90 degrees clockwise around the origin, the new coordinates can be determined using the following transformation:
- The new x-coordinate becomes y (the original y-coordinate).
- The new y-coordinate becomes -x (the negative of the original x-coordinate).
Applying this to the point (4, 3):
- New x-coordinate = 3 (original y-coordinate)
- New y-coordinate = -4 (negative of the original x-coordinate)
Thus, the resulting coordinates after the rotation are (3, -4), making the correct answer D. (3, -4).
To find the number of people per square mile, we need to divide the population by the area. We can perform this division as follows:
Population=3.7×10^7
Area=1.6×10^5
Now, we can divide these two quantities:
People per square mile= (3.7×10^7) ÷ (1.6 × 10^5)
Using the properties of exponents, we can simplify this:
= (3.7 ÷ 1.6) × (10^7 ÷ 10^5) = 3.7 ÷ 1.6 × 10^(7-5) = 3.7 ÷ 1.6 × 10^2
Calculating
3.7 ÷ 1.6 ≈ 2.3125.
Now, multiplying by 10^2 :
2.3125 × 100 ≈ 231.25
Rounding this to the nearest ten gives approximately 240.
Therefore, the best estimate of the number of people per square mile in California is B. 240 people.