Free Online Math Questions Calculator Permitted Exam 2
The gas mileage for Peter’s car is 21 miles per gallon when the car travels at an average speed of 50 miles per hour. The car’s gas tank has 17 gallons of gas at the beginning of a trip. If Peter’s car travels at an average speed of 50 miles per hour, which of the following functions f models the number of gallons of gas remaining in the tank t hours after the trip begins?
What is the value of cos space x ?
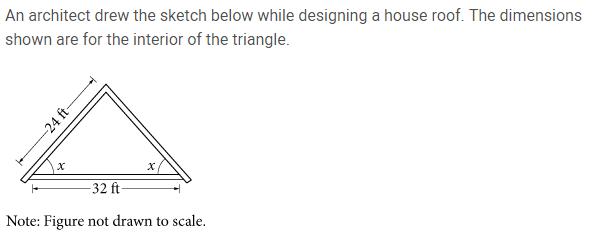



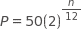
What is A in terms of x?

An international bank issues its Traveler credit cards worldwide. When a customer makes a purchase using a Traveler card in a currency different from the customer’s home currency, the bank converts the purchase price at the daily foreign exchange rate and then charges a 4% fee on the converted cost. Sara lives in the United States, but is on vacation in India. She used her Traveler card for a purchase that cost 602 rupees (Indian currency). The bank posted a charge of $9.88 to her account that included the 4% fee. What foreign exchange rate, in Indian rupees per one U.S. dollar, did the bank use for Sara’s charge? Round your answer to the nearest whole number.
The scatterplot above shows counts of Florida manatees, a type of sea mammal, from 1991 to 2011. Based on the line of best fit to the data shown, which of the following values is closest to the average yearly increase in the number of manatees?
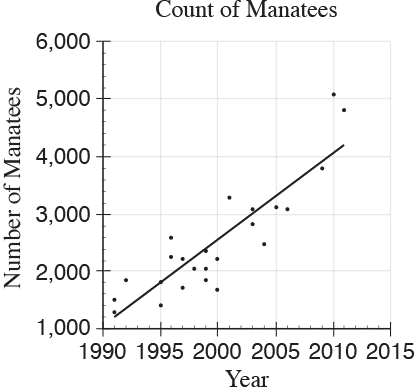
Choice C is correct. The slope of the line of best fit is the value of the average increase in manatees per year. Using approximate values found along the line of best fit (1,200 manatees in 1991 and 4,200 manatees in 2011), the approximate slope can be calculated as fraction numerator 3 comma 000 over denominator 20 end fraction space equals space 150. Choice A is not the correct answer. This value may result from disregarding the actual scale when approximating the slope and interpreting the scale as if each square represents one unit. Choice B is not the correct answer. This value may result from disregarding the actual scale when approximating the slope, and interpreting the scale as if each square along the x-axis represents one year and each tick mark along the y-axis represents 100 manatees. Choice D is not the correct answer. This value may result from disregarding the actual scale along the x-axis when approximating the slope and interpreting each square along the x-axis as one year.
A typical image taken of the surface of Mars by a camera is 11.2 gigabits in size. A tracking station on Earth can receive data from the spacecraft at a data rate of 3 megabits per second for a maximum of 11 hours each day. If 1 gigabit equals 1,024 megabits, what is the maximum number of typical images that the tracking station could receive from the camera each day?
Choice B is correct. The tracking station can receive 118,800 megabits each day left parenthesis fraction numerator 3 space text megabits end text over denominator 1 space text second end text end fraction cross times fraction numerator 60 space text seconds end text over denominator 1 space text minute end text end fraction cross times fraction numerator 60 space text minutes end text over denominator 1 space text hour end text end fraction cross times 11 space text hours end text right parenthesis comma which is about 116 gigabits each day left parenthesis fraction numerator 118.800 over denominator 1 comma 024 end fraction right parenthesis. If each image is 11.2 gigabits, then the number of images that can be received each day is fraction numerator 116 over denominator 11.2 end fraction space almost equal to space 10.4. Since the question asks for the maximum number of typical images, rounding the answer down to 10 is appropriate because the tracking station will not receive a completed 11th image in one day. Choice A is not the correct answer. The student may not have synthesized all of the information. This answer may result from multiplying 3 (rate in megabits per second) by 11 (hours receiving) and dividing by 11.2 (size of image in gigabits), neglecting to convert 3 megabits per second into megabits per hour and to utilize the information about 1 gigabit equaling 1,024 megabits. Choice C is not the correct answer. The student may not have synthesized all of the information. This answer may result from converting the number of gigabits in an image to megabits (11,470), multiplying by the rate of 3 megabits per second (34,410), and then converting 11 hours into minutes (660) instead of seconds. Choice D is not the correct answer. The student may not have synthesized all of the information. This answer may result from converting 11 hours into seconds (39,600), then dividing the result by 3 gigabits converted into megabits (3,072), and multiplying by the size of one typical image.
The toll rates for crossing a bridge are $6.50 for a car and $10 for a truck. During a two-hour period, a total of 187 cars and trucks crossed the bridge, and the total collected in tolls was $1,338. Solving which of the following systems of equations yields the number of cars, x, and the number of trucks, y, that crossed the bridge during the two hours?
Choice C is correct. If x is the number of cars that crossed the bridge during the two hours and y is the number of trucks that crossed the bridge during the two hours, then x space plus space y represents the total number of cars and trucks that crossed the bridge during the two hours, and 6.5 x space plus space 10 y represents the total amount collected in the two hours. Therefore, the correct system of equations is x space plus thin space y space equals space 187 and 6.5 x space plus space 10 y space equals space 1 comma 338. Choice A is not the correct answer. The student may have mismatched the symbolic expressions for total cars and trucks and total tolls collected with the two numerical values given. The expression x space plus space y represents the total number of cars and trucks that crossed the bridge, which is 187. Choice B is not the correct answer. The student may have attempted to use the information that the counts of cars, trucks, and tolls were taken over a period of two hours, but this information is not needed in setting up the correct system of equations. The expression 6.5 x space plus space 10 y represents the total amount of tolls collected, which is $1,338, not fraction numerator text $ end text 1 comma 338 over denominator 2 end fraction. Choice D is not the correct answer. The student may have attempted to use the information that the counts of cars, trucks, and tolls were taken over a period of two hours, but this information is not needed in setting up the correct system of equations. The expression 6.5 x space plus space 10 y represents the total amount of tolls collected, which is $1,338 not text $ end text 1 comma 338 cross times 2.
If k is a positive constant different from 1, which of the following could be the graph of y - x = k ( x + y )in the xy-plane?




If (x,y) is a solution to the system of equations above, what is the value of x² ?
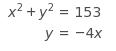
Choice C is correct. The second equation gives y in terms of x, so a student can use this to rewrite the first equation in terms of x. Substituting -4x for y in the equation x squared plus y squared equals 153 gives x squared plus left parenthesis minus 4 x right parenthesis squared equals 153. This can be simplified to x squared space plus space 16 x squared space equals space 153 comma or 17 x squared space equals space 153. Since the question asks for the value of x squared comma not x, dividing both sides of 17 x squared space equals space 153 by 17 gives the answer: x squared space equals space 153 over 17 space equals space 9. Choice A is not the correct answer. This answer may result from neglecting to square the coefficient –4 in y space equals space minus 4 x comma which would give y squared space equals space minus 4 x squared. Then the first equation would become x squared space minus space 4 x squared space equals space minus 3 x squared space equals space 153 comma which would give –51 as the value of x squared. Choice B is not the correct answer. This answer may result from finding the value for x, not the value of x squared. Choice D is not the correct answer. This answer may result from finding the value of y squared comma not x squared.
A researcher places two colonies of bacteria into two petri dishes that each have area 10 square centimeters. After the initial placement of the bacteria left parenthesis t space equals space 0 right parenthesis comma the researcher measures and records the area covered by the bacteria in each dish every ten minutes. The data for each dish were fit by a smooth curve, as shown above, where each curve represents the area of a dish covered by bacteria as a function of time, in hours. Which of the following is a correct statement about the data above?
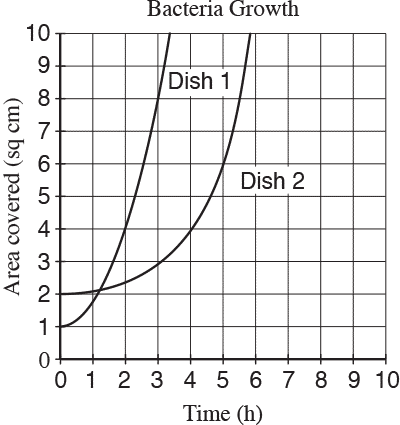

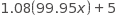
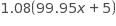
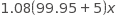
Choice B is the correct answer. Each petri dish has area 10 square centimeters, and so at time t space equals space 0 comma Dish 1 is 10% covered left parenthesis 1 over 10 right parenthesis and Dish 2 is 20% covered left parenthesis 2 over 10 right parenthesis. Thus the statement in B is true. Choice A is not the correct answer. At the end of the observations, both dishes are 100% covered with bacteria, but at time t space equals space 0 comma neither dish is 100% covered. Choice C is not the correct answer. At time t space equals space 0 comma Dish 1 is covered with 50% less bacteria than is Dish 2, but Dish 2 is covered with 100% more, not 50% more, bacteria than is Dish 1. Choice D is not the correct answer. After the first hour, it is still true that more of Dish 2 is covered by bacteria than is Dish 1, but for the first hour the area of Dish 1 that is covered has been increasing at a higher average rate (about 0.8 sq cm/hour) than the area of Dish 2 (about 0.1 sq cm/hour).
When a scientist dives in salt water to a depth of 9 feet below the surface, the pressure due to the atmosphere and surrounding water is 18.7 pounds per square inch. As the scientist descends, the pressure increases linearly. At a depth of 14 feet, the pressure is 20.9 pounds per square inch. If the pressure increases at a constant rate as the scientist’s depth below the surface increases, which of the following linear models best describes the pressure p in pounds per square inch at a depth of d feet below the surface?
Choice B is correct. To determine the linear model, one can first determine the rate at which the pressure due to the atmosphere and surrounding water is increasing as the depth of the diver increases. Calculating this gives fraction numerator 20.9 minus 18.7 over denominator 14 minus 9 end fraction space equals space fraction numerator 2.2 over denominator 5 end fraction comma or 0.44. Then one needs to determine the pressure due to the atmosphere or, in other words, the pressure when the diver is at a depth of 0. Solving the equation 18.7 space equals space 0.44 left parenthesis 9 right parenthesis space plus space b gives b space equals space 14.74. Therefore, the model that can be used to relate the pressure and the depth is p space equals space 0.44 d space plus space 14.74. Choice A is not the correct answer. The rate is calculated correctly, but the student may have incorrectly used the ordered pair left parenthesis 18.7 comma space 9 right parenthesis rather than left parenthesis 9 comma space 18.7 right parenthesis to calculate the pressure at a depth of 0 feet. Choice C is not the correct answer. The rate here is incorrectly calculated by subtracting 20.9 and 18.7 and not dividing by 5. The student then uses the coordinate pair d space equals space 9 and p equals 18.7 in conjunction with the incorrect slope of 2.2 to write the equation of the linear model. Choice D is not the correct answer. The rate here is incorrectly calculated by subtracting 20.9 and 18.7 and not dividing by 5. The student then uses the coordinate pair d space equals space 14 and p space equals space 20.9 in conjunction with the incorrect slope of 2.2 to write the equation of the linear model.
An international bank issues its Traveler credit cards worldwide. When a customer makes a purchase using a Traveler card in a currency different from the customer’s home currency, the bank converts the purchase price at the daily foreign exchange rate and then charges a 4% fee on the converted cost. Sara lives in the United States, but is on vacation in India. She used her Traveler card for a purchase that cost 602 rupees (Indian currency). The bank posted a charge of $9.88 to her account that included the 4% fee. A bank in India sells a prepaid credit card worth 7,500 rupees. Sara can buy the prepaid card using dollars at the daily exchange rate with no fee, but she will lose any money left unspent on the prepaid card. What is the least number of the 7,500 rupees on the prepaid card Sara must spend for the prepaid card to be cheaper than charging all her purchases on the Traveler card? Round your answer to the nearest whole number of rupees.
The figure above shows a metal hex nut with two regular hexagonal faces and a thickness of 1 cm. The length of each side of a hexagonal face is 2 cm. A hole with a diameter of 2 cm is drilled through the nut. The density of the metal is 7.9 grams per cubic cm. What is the mass of this nut, to the nearest gram? (Density is mass divided by volume.)

The question above asks students to make connections between physical concepts such as mass and density and essential geometric ideas such as the Pythagorean theorem and volume formulas. There are multiple approaches to solving this problem, but in any of them, the aim is to find the volume of the metal nut and then use the density of the metal to calculate the mass of the nut (57 grams). This is a multistep problem that requires students to devise a multistep strategy and carry out all the algebraic and numerical steps without error. To solve this problem, students need to find the volume of the hex nut and then use the given fact that density is mass divided by volume. Finding the volume of the hex nut requires several steps. The first step is to calculate the area of one of the hexagonal faces (without the drilled hole). Each face is a regular hexagon, which can be divided into 6 equilateral triangles with side lengths of 2 cm. Using 30-60-90 triangle properties, the height of each equilateral triangle is square root of 3 space end root cm. In turn, the area of one equilateral triangle is 1 half b h equals 1 half left parenthesis 2 right parenthesis left parenthesis square root of 3 right parenthesis equals square root of 3 square cm, so the area of the hexagonal face is 6 square root of 3 square cm. The volume of the hexagonal prism is the area of one face multiplied by the height (or thickness in this case), open parentheses 6 square root of 3 close parentheses open parentheses 1 close parentheses equals 6 square root of 3 cubic cm. Then, to account for the drilled hole, students need to calculate the volume of a cylinder with diameter 2 cm (or radius 1 cm) and height 1 cm, V equals pi r squared h equals pi open parentheses 1 squared close parentheses open parentheses 1 close parentheses equals pi cubic cm, and subtract it from the volume of the hexagonal prism to yield 6 square root of 3 minus pi cubic cm. Finally, density is mass divided by volume, 7.9 equals fraction numerator mass over denominator 6 square root of 3 minus straight pi end fraction. Multiplying both sides of the equation by open parentheses 6 square root of 3 minus straight pi close parentheses yields the mass of the hex nut as 7.9 open parentheses 6 square root of 3 minus straight pi close parentheses grams. When the values for square root of 3 and straight pi are substituted and the result is rounded to the nearest gram, the answer is approximately 57 grams. Note that it is critical for students to attend to the precision of their calculations when solving this problem, and not apply any intermediate rounding until the final answer is reached. Here, the use of a calculator provides the ability to attend to precision more effectively, and thus is highly encouraged.
What is the value of c?




Choice A is correct. The given zeros can be used to set up an equation to solve for c. Substituting –4 for x and 0 for y yields minus 4 c equals 72 comma or c equals minus 18. Alternatively, since –4, 1 half comma and p are zeros of the polynomial function f left parenthesis x right parenthesis equals 2 x cubed plus 3 x squared plus c x plus 8 comma it follows that f left parenthesis x right parenthesis equals left parenthesis 2 x minus 1 right parenthesis left parenthesis x space plus 4 right parenthesis left parenthesis x minus p right parenthesis. Were this polynomial multiplied out, the constant term would be left parenthesis minus 1 right parenthesis left parenthesis 4 right parenthesis left parenthesis minus p right parenthesis equals 4 p. (We can see this without performing the full expansion.) Since it is given that this value is 8, it follows that 4 p equals 8 or rather, p equals 2. Substituting 2 for p in the polynomial function yields f left parenthesis x right parenthesis equals left parenthesis 2 x minus 1 right parenthesis left parenthesis x plus 4 right parenthesis left parenthesis x minus 2 right parenthesis comma and after multiplying the factors one finds that the coefficient of the x term, or the value of c, is –18. Choice B is not the correct answer. This value is a misunderstood version of the value of p, not c, and the relationship between the zero and the factor (if a is the zero of a polynomial, its corresponding factor is x minus a) has been confused. Choice C is not the correct answer. This is the value of p, not c. Using this value as the third factor of the polynomial will reveal that the value of c is -18. Choice D is not the correct answer. This represents a sign error in the final step in determining the value of c.
Which of the following must be true?
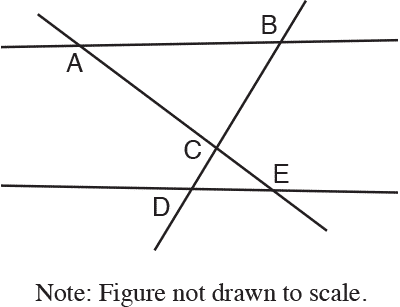




Choice C is correct. Given that triangle A B C is similar to increment E D C, students can determine that the corresponding angle BAC is congruent to angle CED. The converse of the alternate interior angle theorem tells us that stack A B with bar on top parallel to stack D E with bar on top. (Students can also use the fact that angle A B C and angle C D E are congruent to make a similar argument.) Choice A is not the correct answer. This answer may result from multiple misconceptions. The student may have visually identified the segments as perpendicular and used the wrong notation to express this statement. Choice B is not the correct answer. This answer may result from visual inspection of the diagram. The line segments appear to be perpendicular, but need not be, given the information provided. Choice D is not the correct answer. This answer may result from misunderstanding either the notation or the vocabulary of parallel and perpendicular lines. The student has incorrectly identified or notated parallel lines as perpendicular.