Free Math Questions Calculator Not Permitted Exam 3
What is 2y + z in terms of x?
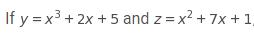




Choice C is correct. Substituting the expressions equivalent to y and z into 2 y plus z results in the expression 2 left parenthesis x cubed plus 2 x plus 5 right parenthesis plus x squared plus 7 x plus 1. The student must apply the distributive property to multiply x cubed plus 2 x plus 5 by 2 and then combine the like terms in the expression. Choice A is not the correct answer. This answer may result if a student correctly finds 2y in terms of x but does not pay careful attention to exponents when adding to x squared plus 7 x plus 1 and then combines the x cubed and x squared terms. Choice B is not the correct answer. This answer may result if a student fails to distribute the 2 when multiplying 2 left parenthesis x cubed plus 2 x plus 5 right parenthesis. Choice D is not the correct answer. This answer may result from a student finding 2 left parenthesis y plus z right parenthesis instead of 2 y plus z.
The mean number of students per classroom, y, at Central High School can be estimated using the equation y=0.8636 x + 27.227 , where x represents the number of years since 2004 and x less or equal than 10. Which of the following statements is the best interpretation of the number 0.8636 in the context of this problem?
Choice D is correct. When an equation is written in the form y equals m x plus b comma the coefficient of the x-term (in this case 0.8636) is the slope. The slope of a linear equation gives the amount that the mean number of students per classroom (represented by y) changes per year (represented by x). Choice A is not the correct answer. This answer may result from a misunderstanding of slope and y-intercept. The y-intercept of the equation represents the estimated mean number of students per classroom in 2004. Choice B is not the correct answer. This answer may result from a misunderstanding of the limitations of the model. Students may see that x less or equal than 10 and erroneously use this statement to determine that the model finds the mean number of students in 2014. Choice C is not the correct answer. This answer may result from a misunderstanding of slope. The student recognizes that slope models the rate of change, but may think that a slope of less than 1 represents a decreasing function.
Which of the following is equal to (14 - 2i) ( 7 + 12i ) ?
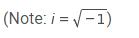
Choice D is correct. Applying the distributive property to multiply the binomials yields the expression 98 plus 168 i minus 14 i minus 24 i squared. The note in the stem of the question reminds students that i equals square root of minus 1 end root comma therefore i squared equals minus 1. Substituting this value into the expression gives the student 98 plus 168 i minus 14 i minus left parenthesis minus 24 right parenthesis comma and combining like terms results in 122 plus 154 i. Choice A is not the correct answer. This answer may result from a combination of errors. The student may not correctly distribute when multiplying the binomials, multiplying only the first terms together and the second terms together. The student may also think that i squared equals 1. Choice B is not the correct answer. This answer may result from a misunderstanding of how to multiply binomials. The distributive property is not applied correctly and the student may only multiply the first two terms together and the last two terms together. Choice C is not the correct answer. This answer results from misapplying the statement i equals square root of minus 1 end root.
Which of the following equations gives a in terms of x ?

Please select 2 correct answers
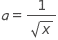
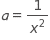


Choice B is correct. There are multiple ways to approach this problem, but all require an understanding of the properties of exponents. The student may rewrite the equation as fraction numerator 1 over denominator square root of a end fraction equals x and then proceed to solve for a first by squaring both sides, which gives 1 over a equals x squared comma and then multiplying both sides by a to find 1 equals a x squared. Finally, dividing both sides by x squared isolates the desired variable. Choice A is not the correct answer. This answer may result from a misunderstanding of the properties of exponents. The student may understand that a negative exponent can be translated to a fraction but misapply the fractional exponent. Choice C is not the correct answer. This answer may result from a misunderstanding of the properties of exponents. A student may recognize that an exponent of 1 half is the same as the square root but misapply this information. Choice D is not the correct answer. This answer may result from a misunderstanding of the properties of exponents. The student may recognize that the fractional exponent on a is the same as the square root, and that therefore a can be isolated by squaring both sides. However, the student may not understand how the negative exponent affects the base.
Which of the following is equal to sin ?
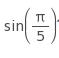


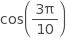
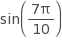
Anise needs to complete a printing job using both of the printers in her office. One of the printers is twice as fast as the other, and together the printers can complete the job in 5 hours. The equation above represents the situation described. Which of the following describes what the expression 1 over x represents in this equation?
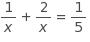
Choice B is correct. From the description given, 1 fifth is the portion of the job that the two printers, working together, can complete in one hour, and each term in the sum on the left side is the part of this 1 fifth of the job that one of the printers contributes. Since one of the printers is twice as fast as the other, 2 over x describes the portion of the job that the faster printer is able to complete in one hour and 1 over x describes the portion of the job that the slower printer is able to complete in one hour. Choice A is not the correct answer. The student may have not seen that in this context, the rates (that is, the work completed in a fixed time) of the printers can be added to get the combined rate, but the times it takes each printer to complete the job cannot be added to get the time for both printers working together, since the time for printers working together is less than, not greater than, the times for each printer alone. Hence the terms in the sum cannot refer to hours worked. In fact, the time it would take the slower printer to complete the whole job is x hours. Choice C is not the correct answer. The student may have seen that 1 over x is the smaller term in the sum, wrongly concluded that the smaller term must apply to the faster printer, and then assumed the 2 in the numerator of the second term implies the equation describes work completed in 2 hours. In fact, the portion of the job that the faster printer could complete in 2 hours is open parentheses 2 close parentheses open parentheses 2 over x close parentheses equals 4 over x. Choice D is not the correct answer. The student may have correctly seen that the value 1 fifth on the right side refers to the portion of the job completed, but not seen that in this context, the rates (that is, the work completed in a fixed time) of the printers can be added to get the combined rate, but the times it takes each printer to complete the job cannot be added to get the time for both printers working together. Hence the terms in the sum cannot refer to hours worked. In fact, the time it takes the slower printer to complete 1 fifth of the job is x over 5 hours.
If line is translated up 5 units and right 7 units, then what is the slope of the new line?
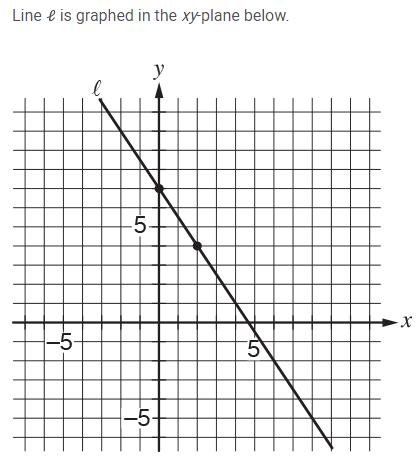



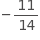
Choice B is correct. The slope of a line can be determined by finding the difference in the y-coordinates divided by the difference in the x-coordinates for any two points on the line. Using the points indicated, the slope is minus 3 over 2. Translating the line moves all the points on the line the same distance in the same direction, and the image will be a parallel line. Therefore, the slope of the image is minus 3 over 2. Choice A is not the correct answer. This value may result from a combination of errors. The student may misunderstand how the negative sign affects the fraction and apply the transformation as fraction numerator left parenthesis minus 3 plus 5 right parenthesis over denominator left parenthesis minus 2 plus 7 right parenthesis end fraction. Choice C is not the correct answer. This value may result from finding the slope of the line and then subtracting 5 from the numerator and 7 from the denominator. Choice D is not the correct answer. This answer may result from adding 5 over 7 to the slope of the line.
What is y in terms of a ?

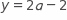

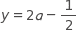
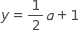
Choice A is correct. Multiplying both sides of the equation by the denominators of the rational expressions in the equation gives 2 y equals 4 a minus 4. The student should then divide both sides by 2 to isolate the y variable, yielding the equation y equals 2 a minus 2. Choice B is not the correct answer. This equation may result if a student does not divide both terms by 2 when isolating y in the equation 2 y equals 4 a minus 4. Choice C is not the correct answer. This equation may result from the student not distributing the 4 when multiplying 4 and open parentheses a minus 1 close parentheses. Choice D is not the correct answer. This equation may result from solving 2 y equals 4 a minus 4 for a comma yielding a equals 1 half y plus 1. A student who does not understand the meaning of the variables may then switch them to match the answer choice.
What is the value of a + 7 ?
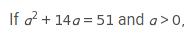
What is the value of 3 x plus 2 y ?
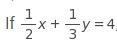
The equation of a circle in the xy-plane is shown above. What is the diameter of the circle?
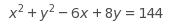
Completing the square yields the equation open parentheses x minus 3 close parentheses squared plus open parentheses y plus 4 close parentheses squared equals 169 comma the standard form of an equation of the circle. Understanding this form results in the equation r squared equals 169 comma which when solved for r gives the value of the radius as 13. Diameter is twice the value of the radius; therefore, the diameter is 26.
What is one possible solution to the equation?
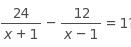
Students should look for the best solution methods for solving rational equations before they begin. Looking for structure and common denominators will prove very useful at the onset, and will help prevent complex computations that do not lead to a solution. In this problem, multiplying both sides of the equation by the common denominator open parentheses x plus 1 close parentheses open parentheses x minus 1 close parentheses yields 24 open parentheses x minus 1 close parentheses minus 12 left parenthesis x plus 1 right parenthesis equals left parenthesis x plus 1 right parenthesis left parenthesis x minus 1 right parenthesis. Multiplication and simplification then yields 12 x minus 36 equals x squared minus 1 comma or x squared minus 12 x plus 35 equals 0. Factoring the quadratic gives open parentheses x minus 5 close parentheses open parentheses x minus 7 close parentheses equals 0 comma so the solutions occur at x equals 5 and x equals 7 comma both of which should be checked in the original equation to ensure that they are not extraneous. In this case, both values are solutions.
If sin w = - a, comma which of the following could be the value of w?





Choice B is correct. If an angle with radian measure x such that straight pi over 2 less than x less than straight pi is placed in standard position, its terminal side will fall in Quadrant II, and sin space x equals a will be the y-coordinate of the point P where its terminal side intersects the unit circle. If sin space w equals minus a comma then when the angle with radian measure w is placed in standard position, its terminal side will intersect the unit circle at a point with y-coordinate equal to minus a. There are two such points on the unit circle: the reflection of P across the x-axis, which would correspond to an angle with radian measure –x (and also with radian measures... minus 6 straight pi minus x comma space minus 4 straight pi minus x comma space minus 2 straight pi minus x comma space 2 straight pi minus x comma space 4 straight pi minus x comma space 6 straight pi minus x space... right parenthesis ; and the reflection of P through the origin, which would correspond to an angle with radian measure x minus straight pi (and also with radian measures ... x space minus space 5 straight pi comma space x minus 3 straight pi comma space x plus straight pi comma space x plus 3 straight pi comma space x plus 5 straight pi... right parenthesis. Thus, of the choices given, only x minus straight pi could be the value of w. Choice A is not the correct answer. In general, sin open parentheses minus x close parentheses equals minus sin space x and sin open parentheses x space plus space straight pi close parentheses equals minus sin space x comma so sin open parentheses straight pi minus straight x close parentheses equals minus sin open parentheses minus x close parentheses equals minus left parenthesis minus sin space x right parenthesis equals sin space x. Therefore, sin open parentheses straight pi minus straight x close parentheses equals a comma not minus a. Choice C is not the correct answer. In general, sin open parentheses 2 straight pi plus x close parentheses equals sin space x comma so sin open parentheses 2 straight pi plus x close parentheses equals a, not minus a. Choice D is not the correct answer. In general, sin open parentheses x minus 2 straight pi close parentheses equals sin space x comma so sin open parentheses x minus 2 straight pi close parentheses equals a comma not minus a.
In the system of linear equations above, a is a constant. If the system has no solution, what is the value of a ?
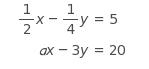

Choice C is correct. If the system of equations has no solution, the graphs of the equations in the xy-plane are parallel lines. To be parallel, the lines must have the same slope, and this will be true if the expression a x minus 3 y is a multiple of the expression 1 half x minus 1 fourth y. Since minus 3 y equals 12 open parentheses minus 1 fourth y close parentheses comma the expression a x minus 3 y would have to be 12 times the expression 1 half x minus 1 fourth y. This means a x equals 12 open parentheses 1 half x close parentheses comma so a equals 6. The resulting system is 1 half x minus 1 fourth y equals 5 and 6 x minus 3 y equals 20 comma which is equivalent to 6 x minus 3 y equals 60 and 6 x minus 3 y equals 20 comma which has no solution. Choice A is not the correct answer. This may result from the misconception that if each equation in a system has the same x-coefficient, the system cannot have a solution. But if a equals 1 half comma subtracting the two equations eliminates x and produces a solution to the system. Choice B is not the correct answer. This may result from trying to make the second equation in the system a multiple of the first by looking at the ratio of the constants on the right sides, 20 over 5 comma and wrongly concluding that the second equation must be 4 times the first, which would give a equals 4 open parentheses 1 half close parentheses comma or a equals 2. But the two equations in a system are multiples only if the system has infinitely many solutions, not if the system has no solution. Choice D is not the correct answer. The student may have found the factor, 12, that multiplies the left side of the first equation to yield the left side of the second, but then neglected to find a equals 12 open parentheses 1 half close parentheses comma or a equals 6.
Based on the system of equations above, what is the value of the product xy?
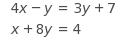




Choice C is correct. There are several solution methods possible, but all involve persevering in solving for the two variables and calculating the product. For example, combining like terms in the first equation yields 4 x space minus space 4 y space equals space 7 and then multiplying that by 2 gives 8 x space minus space 8 y space equals space 14. When this transformed equation is added to the second given equation, the y-terms are eliminated, leaving an equation in just one variable: 9 x equals 18 comma or x equals 2. Substituting 2 for x in the second equation (one could use either to solve) yields 2 plus 8 y equals 4 comma which gives y equals 1 fourth. Finally, the product xy is 2 cross times 1 fourth equals 1 half. Choice A is not the correct answer. Students who select this option have most likely made a calculation error in transforming the second equation (using minus 4 x minus 8 y equals minus 16 instead of minus 4 x minus 32 y equals minus 16) and used it to eliminate the x-terms. Choice B is not the correct answer. This is the value of y for the solution of the system, but it has not been put back into the system to solve for x to determine the product xy. Choice D is not the correct answer. Not understanding how to eliminate a variable when solving a system, a student may have added the equations 4 x minus 4 y equals 7 and x plus 8 y equals 4 to yield 5 x space plus space 4 y space equals space 11. From here, a student may mistakenly simplify the left-hand side of this resulting equation to yield 9 x y equals 11 and then proceed to use division by 9 on both sides in order to solve for xy.
The graph of y =(2 x - 4 )( x - 4 ) is a parabola in the xy-plane. In which of the following equivalent equations do the x- and y-coordinates of the vertex of the parabola appear as constants or coefficients?
Please select 2 correct answers



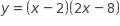
What is the distance between the chord and the diameter in terms of r?

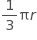


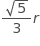
Choice D is correct. This represents the length of the distance between the chord and the diameter, using a radius of the circle to create a triangle, and then the Pythagorean theorem to solve correctly: r squared equals x squared plus open parentheses 2 over 3 r close parentheses squared comma where r represents the radius of the circle and x represents the distance between the chord and the diameter. Choice A is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have tried to use the circumference formula to determine the distance rather than making use of the radius of the circle to create a triangle. Choice B is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have tried to use the circumference formula to determine the distance rather than making use of the radius of the circle to create a triangle. Choice C is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have made a triangle within the circle, using a radius to connect the chord and the diameter, but then may have mistaken the triangle for a 45-45-90 triangle and tried to use this relationship to determine the distance.
In the equation above, what is the value of k?
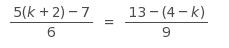




Choice B is correct. Simplifying the numerators yields 5 k + 3 over 6 = 9 + k over 9 , and cross multiplication gives 45 k + 27 = 54 + 6 k. Solving for k yields k = 9 over 13. Choice A is not the correct answer. This value may result from not correctly applying the distributive property on the right-hand side, resulting in the expression 13 - 4- k in the numerator. Correctly applying the distributive property yields 13 - ( 4 - k) = 13 - 4 + k in the numerator. Choice C is not the correct answer. This value may result from not correctly applying the distributive property on the left-hand side, resulting in the expression 5 k + 2 - 7. Correctly applying the distributive property yields 5 ( k + 2 ) - 7 = 5 k + 3 in the numerator. Choice D is not the correct answer. This value may result from not using the appropriate order of operations when simplifying either numerator.