FREE MAP HS Math Questions and Answers
Which of the following statements most accurately depicts the line's grid equation and its relationship to the y-axis?
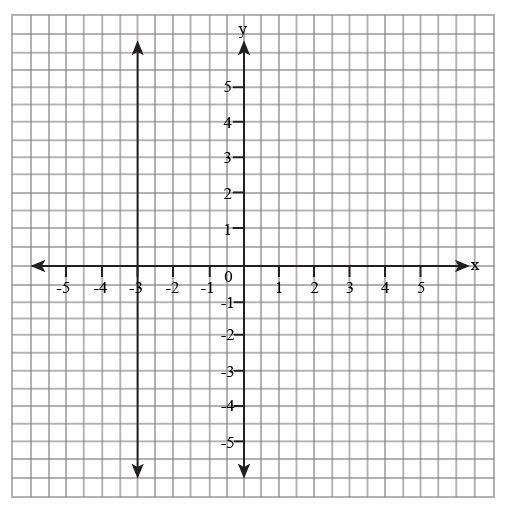
The graph indicates that the specified line is perpendicular to the x-axis and parallel to the y-axis. Furthermore, the line that crosses the x-axis at x = -3.
So, the equation of the line is x = -3.
In a grocery store, a customer purchased 58 products for a total of $4.20. Bananas made up the majority of the products, with some apples included.
• Each apple costs $0.05
• Each banana costs $0.10
Which set of equations may be used to determine, from the customer's purchases at the grocery shop, a) the number of apples and b) the number of bananas?
There are a few apples and bananas among the 58 total items.
Represent this condition algebraically as follows:
a + b = 58
The buyer must next fulfill the remaining requirement, which is $4.20. In this instance, an apple costs $0.05 while a banana costs $0.10.
SGiven that there are apples and that each one costs $0.05, the outcome is $0.05a.
Because there are b bananas and they each cost $0.10, $0.10b is the outcome.
Represent the above condition algebraically as follows:
0.05a + 0.10b = 4.20
Which of the following inequality best characterizes the part's range and domain?
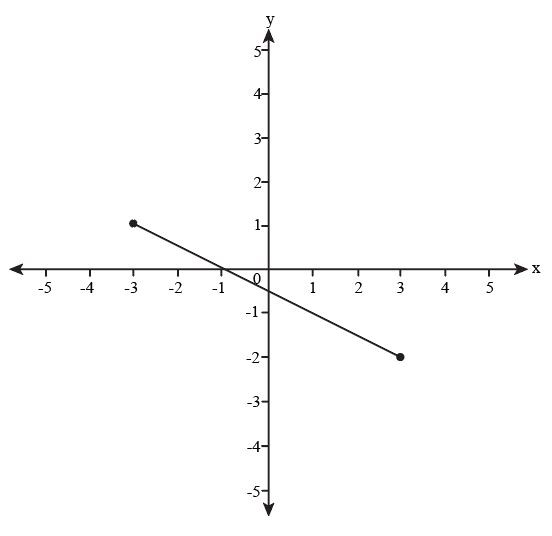
Remember that the function's domain includes all values that the x-axis line covers. The line on the graph spans the x-axis from -3 to 3..
So, the domain will be -3 ≤ x ≤ 3.
Additionally, keep in mind that the function's range includes any values that are covered by the y-axis line.
The line graph, as seen in the graph, spans the y-axis from -2 to 1..
Thus, the range of the function is -2 ≤ x ≤ 1.
What expression can be used in place of 64x2 – 225?
Make the expression simpler 64x² – 225
64x²– 225 = (8x)² – (15)²
Recall the identity (a + b)(a – b) = a² – b². So, a = 8x and b = 15.
Thus, (8x)² – (15)² = (8x – 15)(8x + 15).
Which of the following best depicts the equation of the line that crosses (32,24) and (-10,-8)?
Which of the following represents 6x² – 17x + 5 in factored form?
Examine the quadratic expression provided 6x² – 17x + 5.
Factorize the following expression:
6x² – 17x + 5 = 6x² – 15x – 2x + 5
6x² – 17x – 5 = 3x(2x – 5) – 1(2x – 5)
6x² – 17x – 5 = (2x – 5)(3x – 1)
Thus, the factored form is (2x – 5)(3x – 1).
Take a look at the function f(x) = x² – 9x + 20.
Which of these claims about the following is true?
The given function is as follows:
f(x) = x² – 9x + 20
Factorize the given function as follows:
f(x) = x² – 9x + 20
f(x) = x² – 4x – 5x + 20
f(x) = x(x – 4) – 5(x – 4)
f(x) = (x – 4)(x – 5)
The factors are (x – 4) and (x – 5).
Now, find the zeros as follows:
(x – 4)(x – 5) = 0
Thus, the zeros are x = 4, and x = 5.
What phrase can be used in place of √176?
Construct 176's prime factorization as follows:
176 = 2 × 2 × 2 × 2 × 11
Assign the prime factors in pairs:
176 = (2 × 2) × (2 × 2) × 11
Now, calculate both sides' positive square roots:
√176 = √((2 × 2) × (2 × 2) × 11)
√176 = 4√11
Therefore, √176 = 4√11.
In the solution set of -5x – 25y < -30, which of the following ordered pairs is present?
The given inequality is -5x – 25y < -30.
Consider the point (6,0). Take this point and check the inequality as follows:
-5(6) – 25(0) < -30
-30 < -30
This is false. So, (6,0) cannot be the solution.
Consider the point (21,-3). Take this point and check the inequality as follows:
-5(21) – 25(-3) < -30
-105 + 75 < -30
-30 < -30
This is false. So, (21,-3) cannot be the solution.
Consider the point (4,-3). Take this point and check the inequality as follows:
-5(4) – 25(-3) < -30
55 < -30
This is false. So, (4,-3) cannot be the solution.
Consider the point (5,1). Take this point and check the inequality as follows:
-5(5) – 25(1) < -30
-50 < -30
This is true. So, (5,1) is the solution.
Which of the following expressions is 9x² + 72x + 144?
The given expression is 9x² + 72x + 144.
Recall the identity (a + b)² = a² + 2ab + b².
Write the expression in the identity form as follows:
9x² + 72x + 144 = (3x)² + 2 ∙ 3x ∙ 12 + (12)²
9x² + 72x + 144 = (3x + 12)²