PMF (Probability Mass Function): A Comprehensive Guide
In the world of statistics, the Probability Mass Function (PMF) is key. It helps understand discrete random variables. This guide looks into what the PMF is, how it’s used, its features, and how it connects with different distributions, such as the Binomial, Poisson, Geometric, and Negative Binomial distributions.
The PMF is all about the probability pattern of a discrete random variable. This is different from continuous ones that can be any value within a set. PMF is important in coding and stats because it links chances of events happening. It’s crucial in hypothesis testing, good-fit tests, and categorical data checks.
Free PMF Practice Test Online
For the PMF to work, it has to meet two rules: Px (x) ≥ 0 and ∑xϵRange(x) Px (x) = 1. This makes sure that all outcomes together have a 100% chance. Using PMF helps find the averages and differences in odds for a discrete set of results.
The PMF is everywhere, from Bernoulli trials and binomial distribution to Poisson and hypothesis testing. It tells us the chances of certain events, like successful sales calls or defective products. You can also use it to guess how many people will show up at a bank. It’s handy for checking the odds of specific things happening, like typos in a book.
Key Takeaways
- The Probability Mass Function (PMF) is a statistical tool that characterizes the probability distribution of discrete random variables.
- The PMF must satisfy the conditions Px (x) ≥ 0 and ∑xϵRange(x) Px (x) = 1, ensuring that the probabilities assigned to discrete outcomes sum up to 1.
- The PMF is used in computer programming and statistical modeling to relate discrete events to their associated probabilities.
- The PMF is the primary component in defining discrete probability distributions, including the Binomial, Poisson, Geometric, and Negative Binomial distributions.
- The PMF is applied in various fields, such as Bernoulli trials, binomial distribution, Poisson distribution, and hypothesis testing.
The PMF is everywhere, from Bernoulli trials and binomial distribution to Poisson and hypothesis testing. It tells us the chances of certain events, like successful sales calls or defective products. You can also use it to guess how many people will show up at a bank. It’s handy for checking the odds of specific things happening, like typos in a book.
Understanding Probability Mass Function
The Probability Mass Function (PMF) shows the chance of each outcome for a discrete random variable. This is different from continuous variables, which can have any value in a range. Discrete ones have a set number of options or an endless list of options.
What is a Probability Mass Function?
The probability mass function (PMF) for a discrete variable $X$ is written as $P_X(x_k) = P(X=x_k)$. Here, $k$ stands for any counting number and $x_k$ is one of the possible values of $X$. This function tells us the chance $X$ will be exactly $x_k$.
Discrete Random Variables
Examples of discrete variables include the outcome of Bernoulli trials or using the binomial and Poisson distributions. These variables are used in many places for probability calculations, data analysis, and statistical inference.
Properties of PMF
The probability mass function has some key features:
- For all $x$ that $X$ can be, $P_X(x)$ is between 0 and 1.
- All possible outcomes of $X$ together means they add up to 1 in probability.
- The probability $X$ is in a certain group from the range is just the sum of those specific
Understanding these PMF properties is vital for many things. They help with making models for chances, testing ideas, and using stats in various fields.
PMF (Probability Mass Function) Test
The PMF (Probability Mass Function) test helps check if observed data fits a predicted distribution. It’s very handy when working with discrete probability distributions, like the Binomial, Poisson, Geometric, and Negative Binomial.
Binomial Distribution PMF
For the binomial distribution, we use the PMF $P_X(x) = \binom{n}{x} p^x (1-p)^{n-x}$. Here, $n$ is the trials, $x$ the successes, and $p$ the success chance. It’s great for figuring success count in fixed Bernoulli trials.
Poisson Distribution PMF
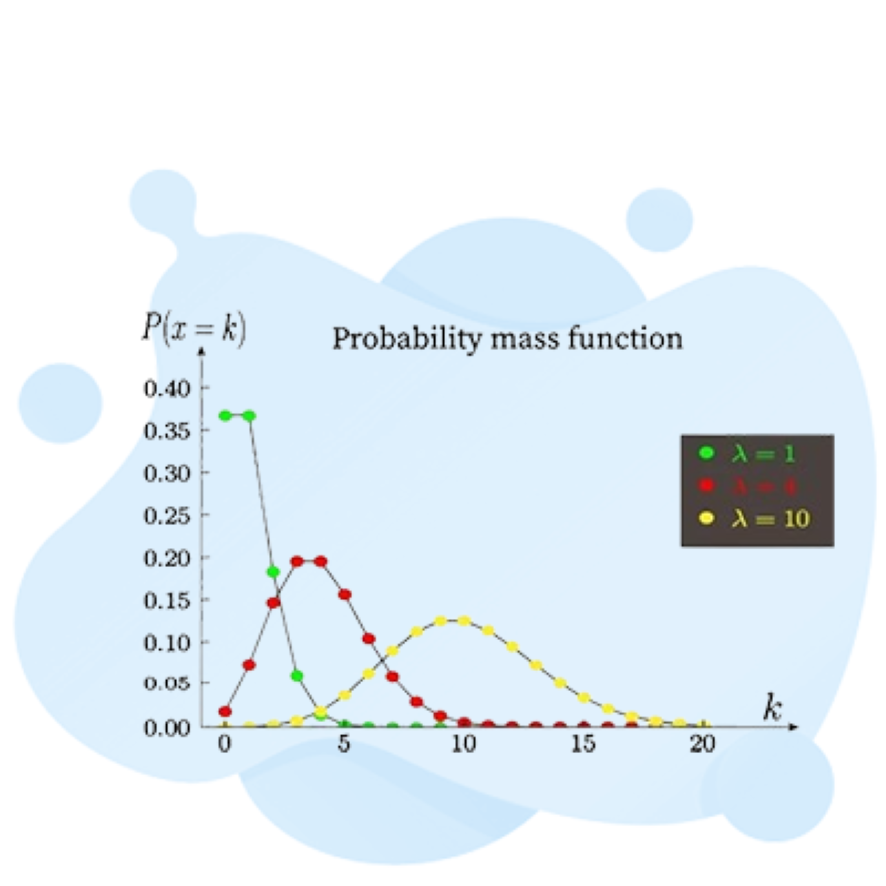
The Poisson distribution deals with events over a set time or space. Its PMF is $P_Y(y) = \frac{e^{-\lambda}\lambda^y}{y!}$. $y$ means event count, and $\lambda$ is the average events number.
Geometric Distribution PMF
The geometric distribution tells us how many trials we need for the first success. Its PMF is $P_Z(z) = p(1-p)^{z-1}$. $z$ tracks trial count, and $p$ is success chance for each trial.
Negative Binomial Distribution PMF
Then, the negative binomial distribution describes trials needed for set successes. Its PMF is $P_W(w) = \binom{w-1}{r-1} p^r (1-p)^{w-r}$. For this, $w$ is the trial count, $r$ the success goal, and $p$ success probability.
These distributions and their PMFs are crucial for statistical hypothesis testing. They’re key for goodness-of-fit tests and categorical data analysis. Knowing them well helps researchers and analysts model and understand specific data types, leading to better decisions.
Applications and Examples
The Probability Mass Function (PMF) is useful in many areas. It helps with things like risk analysis and traffic models. This also includes gaming and finance. Researchers and analysts use discrete probability distributions this way to solve problems. They tackle statistical hypothesis testing and do goodness-of-fit tests.
Modeling Discrete Phenomena
The PMF is key for things we can count. For example, how many times we see a result in a series of tries. It’s used for coin flips and figuring out employee gender. It’s also good for knowing how often we expect to see certain events. This could be monthly product demands or customer arrivals. Using the right tools, like discrete probability distribution, helps get important information.
Statistical Hypothesis Testing
In statistical hypothesis testing, the PMF helps check if data fits a certain pattern. Tests like the chi-square test look at how the data matches what we expect. They are useful in many fields. This includes looking at specific data types or checking on how tests and it includes checking on how tests that need certain assumptions are doing.
Goodness-of-Fit Tests
Tests like the chi-square test see how well data matches a theoretical pattern. This checks if data is following an expected pattern. It’s good for things like the binomial distribution or the Poisson distribution. These methods help figure out likelihood estimation and sampling distribution. They help with probability calculations and data analysis.
Practical Examples from Various Fields
The Probability Mass Function has uses in many fields, such as:
- Finance: Looking into loan defaults, stock changes, and financial risk.
- Marketing: Making guesses about losing customers, checking on campaign success, and sales forecasts.
- Engineering: Checking on reliability, quality control, and finding problems in making things.
- Biology: Understanding traits, how populations change, and why some species are more common.
- Transportation: Predicting traffic, when vehicles arrive, and improving moving things.
Using the Probability Mass Function lets people in these fields improve decision-making. They get more out of their data by using statistical inference.
Conclusion
We’ve covered a lot on the Probability Mass Function (PMF) in this guide. It’s a key tool for working with discrete random variables. We looked into what PMFs are and how they relate to certain probability distributions.
Understanding PMF is crucial for fields like risk analysis and gaming. It helps in decision-making and making sense of data. PMF is valuable for data analysts and researchers.
In wrapping up our discussion on PMF, we see its value. It’s a must-have for anyone working with data today. PMF opens new doors for professionals, allowing them to lead change in their areas.
FAQ
What is a Probability Mass Function (PMF)?
The PMF is a math function for a discrete random variable’s probability distribution. It shows the chance of a variable having a certain value.
Unlike continuous variables that can be any value within a range, the PMF deals with specific values.
How does a PMF differ from a Probability Density Function (PDF)?
The PMF works with discrete variables, and the PDF works with continuous ones. For instance, tossing a coin is discrete, while measuring rainfall is continuous.
It gives the probability of certain values for the PMF, while the PDF shows the density of probabilities in a range of values.
What are the properties of a PMF?
A PMF should follow two main rules. First, all its probabilities need to add up to 1. Second, probabilities can’t be negative.
What are some common discrete probability distributions described by a PMF?
Distributions like Binomial, Poisson, Geometric, and Negative Binomial are often described by a PMF.
What is the PMF (Probability Mass Function) test?
The PMF test checks how well theoretical and actual data match for discrete distributions. It’s great for looking at Binomial, Poisson, Geometric, and Negative Binomial fits.
What are the applications of the Probability Mass Function (PMF)?
PMF is used in many areas like risk analysis, traffic, games, and finance. It helps model and analyze various random events.

