HiSET Math Practice Quiz 3
A rate in which the second quantity in the comparison is one unit.
Two angles whose sum is 180 degrees.
Two angles whose sum is 180 degrees are called "supplementary angles." When two angles are supplementary, they form a straight angle, which is a straight line.
Mathematically, if two angles are labeled as angle A and angle B, and they are supplementary, their relationship can be expressed as:
A + B = 180 degrees
Supplementary angles are important in geometry and trigonometry. For example, when two lines intersect, the adjacent angles (angles next to each other) formed on one side of the intersection are supplementary. In trigonometry, the concept of supplementary angles is used in various calculations and proofs involving trigonometric functions.
A point where two or more straight lines meet.
What percentage of students who got a mark below 30 got a mark below 20?
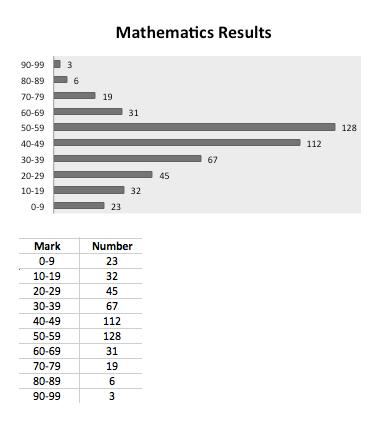
The number of students who got a mark less than 30 was 23 + 32 + 45 = 100. The number of students who got a mark less than 20 was 23 + 32 = 55. The percentage of students who got a mark less than 30 who got a mark less than 20 was 55÷100 = 55%.
Any real number which cant be expressed as a fraction of two integers.
Any real number that cannot be expressed as a fraction of two integers is called an "irrational number." These numbers cannot be represented as the quotient of two whole numbers, and their decimal expansions go on infinitely without repeating any pattern.
A figure formed by two rays with a common endpoint.
An angle is a geometric figure formed by two rays that have a common endpoint, called the vertex. The two rays, also known as the sides of the angle, spread out from the vertex in different directions. Angles are used to measure the amount of rotation or separation between the two rays.
What is the probability that if you randomly picked two students who sat for the examination you would find they both got a mark of 70 or better?
There were 466 students who sat for the examination. The number who got a mark of 70 or more was 28. The probability of the first student getting a mark of 70 or better is 28/466 . The probability of the second student getting a mark of 70 or better is 27/465 . The probability of both getting a mark of 70 or better is 28/466 x 27/465 .
Which is the best simplification of (24 x 32) / (2 x 3)?
(24 x 32) / (2 x 3)= 24-1 × 32-1. 24-1 × 32-1 = 23 × 31 23 × 31 = 23 × 3
Which of the following is the same as (√3 + √2)2 ?
(√3 + √2)2 = (√3 + √2)( √3 + √2) (√3 + √2)( (√3 + √2) = √3×√3 + √3×√2 + √2×√3 + √3×√3 √3×√3 + √3×√2 + √2×√3 + √3×√3 = 3 + √6 + √6 + 2 3 + √6 + √6 + 2 = 5 + 2√6
What is the value of (x2 + x + 3) / (x + 2) when x = -1?
(x2 + x + 3) / (x + 2) = ( (-1)2 + (-1) + 3) / ((-1) + 2) when x=-1 ( (-1)2 + (-1) + 3) / ((-1) + 2) = (1 - 1 + 3)/ (-1 + 2) (1 - 1 + 3)/ (-1 + 2) = 3 / 1 = 3
Results that senior students from a large high school received in an international mathematics examination. A pass in this examination is regarded as a mark of 40 or more. How many students in this high school failed to pass this mathematics examination?

The mark categories indicating failure are 0-9, 10-19, 20-29 and 30-39. The number of marks in those categories was 23, 32, 45 and 67. 23 + 32 + 45 + 67 = 167. The number of students who failed the examination was 167.
A segment whose endpoints are on a circle.
A segment whose endpoints lie on a circle is indeed called a "chord" of the circle. Chords are essential elements of a circle, and they help define various properties and theorems related to circles in geometry.
Which of the following mark intervals contains the highest percentage of students who sat this examination?

The largest number in a mark interval shown is 128. The interval associated with this number is 50-59. The number of students in the mark interval 10-29 is 32 + 45 = 77. 128 is greater than 77. Of the mark intervals shown the highest percentage of students who sat this examination was in the 50-59 interval.
The number of students who sat the examination was 466. What is true about the median mark obtained by students who sat this examination?

As there are 466 students the median will be found by averaging the 233rd and 234th marks, after the marks have been placed in order. Both the 233rd and 234th marks will lie somewhere from 40 to 49. The average of these two marks will lie somewhere from 40 to 49.
One of two equal factors of a number.
Which of the following is the same as 10x2 - 11x + 3?
10x2 - 11x + 3 = 10x2 - 5x - 6x + 3 10x2 - 5x - 6x + 3 = 5x(2x - 1) - 3(2x - 1) 5x(2x - 1) - 3(2x - 1) = (5x - 3)(2x -1)