FREE Traffic Enforcement Mathematical Reasoning Question and Answers
What was the difference between year five and year six's total bench and table production?
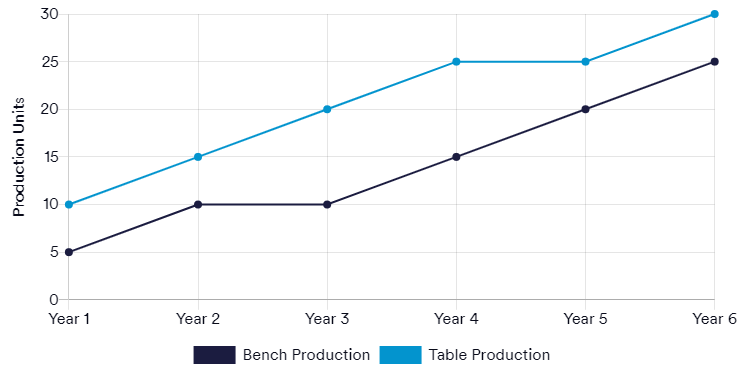
Explanation:
We need to add the values from Year 5 and subtract it from the total value in year 6:
25 + 20 = 45
30 + 25 = 55
55 - 45 = 10
What percentage of those who took the test were unemployed, on average?
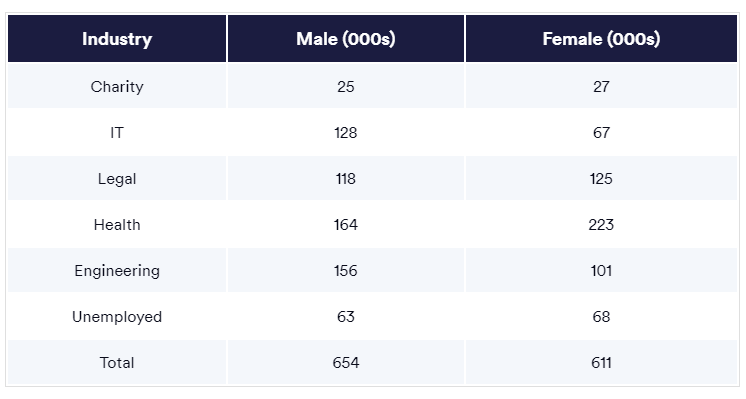
Explanation:
Male total = 654
Female total = 611
Total = 654 + 611 = 1,265
Total unemployed: 63 + 68 = 131
Percentage unemployed: (131 / 1,265) x 100 = 10%
What percentage of Health employees would be female in three years if the number of women working there rises by 10% annually while the number of men stays the same?

Explanation:
Female employees
223 x 1.1 = 245
245 x 1.1 = 270
270 x 1.1 = 297
Male employees
164
Total employees
297 + 164 = 461
Female percentage: (297 / 461) x 100 = 64.4%
What proportion of total output did benches make up throughout the course of the six years?

Explanation:
To determine the answer to this query, we must first determine the total number of items produced, after which we must determine what proportion the total number of benches represents:
Total Tables = 125,000
Total Benches = 85,000
125,000 + 85,000 = 210,000
85,000 / 210,000 x 100 = 40.5
What percentage of men to women are unemployed?

Explanation:
To find the answer double both genders’ figures:
63:68
126:136
Assume that year three's total production costs were £150,000. How much did it cost to produce one bench if one table cost £2.50 to make?

Explanation:
We must calculate the cost of producing 20,000 tables at a cost of £2.50 to discover the answer. The remaining cost must then be divided by the 10,000 benches to see how much is left:
2.50 x 20,000 = 50,000
150,000 - 50,000 = 100,000
100,000 / 10,000 = 10
How many more men will work in the industry if there is a 20% increase in female engineers next year but no change in the number of men?

Explanation:
Female engineers
101,000 x 1.2 = 121.200
Male engineers: 156,000
Difference: 156,000 – 121,200 = 34,800