FREE Pre-Calculus Polynomial Functions Questions and Answers
What is the degree of P(x)=3x^4-7x^2-2x^7-x+4 polynomial function?
The degree of a polynomial function is determined by the highest exponent of the variable in the expression. In the given polynomial function P(x) = 3x^4 - 7x^2 - 2x^7 - x + 4, the term with the highest exponent of x is -2x^7, making the degree of the polynomial 7. Therefore, the correct answer is 7.
The equation f(x) = 5x^4-8x^3+4x^2-6x+3 has how many roots or zeros?
The number of roots or zeros of a polynomial function is equal to the degree of the polynomial. In the given function f(x) = 5x^4 - 8x^3 + 4x^2 - 6x + 3, the highest exponent of x is 4, which means it is a quartic function, and quartic functions have 4 roots. Therefore, the correct answer is 4.
P(x) = x^3+6x^2+9x+54 has a polynomial function; find all its zeros.
To find the zeros of the polynomial function P(x) = x^3 + 6x^2 + 9x + 54, we set P(x) equal to zero and solve for x. By factoring or using other methods, we find the zeros are x = -6, x = 3i, and x = -3i. Therefore, the correct answer is -6, 3i, -3i.
What is another term for the point where a function intersects the x-axis?
All of these terms refer to the same concept—the point where a function intersects the x-axis. Whether it's called an "x-intercept," "zero," or "root," they all signify the value(s) of x for which the function equals zero.
The polynomial can be represented as...
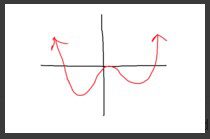
The given polynomial is of the form of an even degree polynomial, as it contains only even power terms (like x^2, x^4, etc.), and it has a positive leading coefficient (the coefficient of the highest-degree term). Therefore, the correct answer is "Even degree, positive leading coefficient."
What degree is shown in the picture?
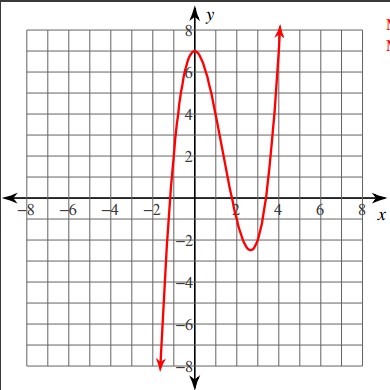
The degree of a polynomial is determined by the highest exponent of the variable in the expression. In this case, since the degree of the polynomial is odd, it means the highest exponent of the variable is an odd number. Therefore, the correct answer is "Odd."
Classify based on the Degree: 4x^3 - 5x^2 + 2x - 1
The degree of a polynomial is determined by the highest exponent of the variable in the expression. In the given polynomial 4x^3 - 5x^2 + 2x - 1, the term with the highest exponent of x is 4x^3, making the degree of the polynomial 3. Therefore, the correct answer is "3."
Advertisement
f(x) = 2x^3 - 3x^2 + 4x -10 How many degrees does f(x) have?
The degree of a polynomial is determined by the highest exponent of the variable in the expression. In the given polynomial f(x) = 2x^3 - 3x^2 + 4x - 10, the term with the highest exponent of x is 2x^3, making the degree of the polynomial 3. Therefore, the correct answer is "3."
f(x) = -3x^4 + x^3 - 2x^2 + x - 1 How many degrees does f(x) have?
The degree of a polynomial is determined by the highest exponent of the variable in the expression. In the given polynomial f(x) = -3x^4 + x^3 - 2x^2 + x - 1, the term with the highest exponent of x is -3x^4, making the degree of the polynomial 4. Therefore, the correct answer is "4."
Given: f(x) = -3x^4 + x^3 - 2x^2 + x - 1, What is the y-intercept of f(x)?
The y-intercept of a function is the point where the graph intersects the y-axis, and it occurs when x is equal to 0. In the given polynomial f(x) = -3x^4 + x^3 - 2x^2 + x - 1, when x is 0, the y-value is -1, making the y-intercept (0, -1). Therefore, the correct answer is (0, -1).
Determine the zeros of f(x) if f(x) = x^3 - 3x^2 - 4x.
To find the zeros of a polynomial function f(x), we set f(x) equal to zero and solve for x. In the given polynomial f(x) = x^3 - 3x^2 - 4x, we can factor it as f(x) = x(x^2 - 3x - 4). Setting each factor equal to zero, we find the zeros of the function as x = -1, x = 0, and x = 4. Therefore, the correct answer is {-1, 0, 4}.
f(x) = x3 - 9x^2 - 45x - 27 : Determine the remaining zeros if -3 is a zero of f(x).
To find the remaining zeros of the polynomial function f(x) = x^3 - 9x^2 - 45x - 27 given that -3 is a zero, we can use synthetic division or long division to divide f(x) by (x + 3). Doing so, we get a quadratic expression x^2 - 6x + 9, which can be factored as (x - 3)^2. Therefore, the remaining zeros are the solutions to (x - 3)^2 = 0, which are x = 3 and x = 6 ± 3√5. The correct answer is {-3, 6 ± 3√5}.
Determine whether (x-3) is a factor of (3x^3+10x^2-x-12)
To determine if (x - 3) is a factor of the polynomial (3x^3 + 10x^2 - x - 12), we can use synthetic division or long division. When we perform synthetic division or long division, we find that the remainder is not zero, indicating that (x - 3) is not a factor of the polynomial. Therefore, the correct answer is "No, it is not a factor."
Determine the roots of the following: Solve (n-2)(4n+3)=0
To find the roots of the equation (n - 2)(4n + 3) = 0, we set each factor equal to zero and solve for n. The roots are the values of n that make the equation true. Setting (n - 2) = 0, we get n = 2, and setting (4n + 3) = 0, we get n = -3/4. Therefore, the correct answer is (-3/4, 2) since both values of n satisfy the equation.
Advertisement
Determine all the factors of x^3 -3x^2 -4x +12 if -2 is a zero.
If -2 is a zero of the polynomial x^3 - 3x^2 - 4x + 12, it means that (x + 2) is a factor. To find the other factors, we can perform polynomial division, which results in (x^3 - 3x^2 - 4x + 12) divided by (x + 2) equaling x^2 - 5x + 6. We can then factor x^2 - 5x + 6 as (x - 2)(x - 3). Therefore, the correct answer is (x - 2)(x + 2)(x - 3), which are all the factors of the given polynomial.
The zeros of a polynomial function with rational coefficients are 3 + 5 and i. Find all additional zeros.
Since the polynomial has rational coefficients, complex zeros come in conjugate pairs. Given the zeros 3 + √5 and i, the additional zeros must be the conjugates of these: −3 - √5 and -i. Therefore, the correct answer is −3 - √5 and i.