FREE CMAS Mathematics Questions and Answers
What fraction of the total surveyed students play a sport?
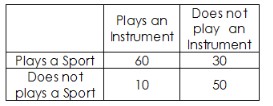
So, the total number of students who play a sport is:
Total who play a sport = Students who play both + Students who only play a sport = 60 + 10 = 70
Now, we know there were 150 students surveyed in total. Therefore, the fraction of students who play a sport is:
Fraction = Number of students who play a sport ÷ Total number of surveyed students = 1/5
Fraction = 70 ÷ 150 = 7/15
The correct answer for the fraction of students who play a sport is 7/15.
The point (4, 3) is rotated 90 degrees clockwise about the origin. What are the coordinates of the resulting point?
To rotate a point (x, y) 90 degrees clockwise around the origin, the new coordinates can be determined using the following transformation:
- The new x-coordinate becomes y (the original y-coordinate).
- The new y-coordinate becomes -x (the negative of the original x-coordinate).
Applying this to the point (4, 3):
- New x-coordinate = 3 (original y-coordinate)
- New y-coordinate = -4 (negative of the original x-coordinate)
Thus, the resulting coordinates after the rotation are (3, -4), making the correct answer D. (3, -4).
150 students were surveyed and asked whether they played a sport and whether they played a musical instrument. The results are shown in the table above.

From the table, we see that 30 students play an instrument but do not play a sport.
Now, we can find the fraction of students who play an instrument but do not play a sport:
Fraction = 30 ÷ 90 = 1/3
However, since we need the total number of students surveyed to calculate the fraction of those who play an instrument but do not play a sport relative to the total number of students (150):
Fraction = 30 ÷ 150 = 1/5
The correct answer for the fraction of students who play an instrument but do not play a sport is 1/5.
Which of the following is an integer?
An integer is a whole number that can be positive, negative, or zero, but it cannot be a fraction or a decimal.
The population of California is approximately 3.7 x 10^7 people. The land area of California is approximately 1.6 x 10^5 square miles. Divide the population by the area to find the best estimate of the number of people per square mile in California.
To find the number of people per square mile, we need to divide the population by the area. We can perform this division as follows:
Population=3.7×10^7
Area=1.6×10^5
Now, we can divide these two quantities:
People per square mile= (3.7×10^7) ÷ (1.6 × 10^5)
Using the properties of exponents, we can simplify this:
= (3.7 ÷ 1.6) × (10^7 ÷ 10^5) = 3.7 ÷ 1.6 × 10^(7-5) = 3.7 ÷ 1.6 × 10^2
Calculating
3.7 ÷ 1.6 ≈ 2.3125.
Now, multiplying by 10^2 :
2.3125 × 100 ≈ 231.25
Rounding this to the nearest ten gives approximately 240.
Therefore, the best estimate of the number of people per square mile in California is B. 240 people.