Τεστ Γνώσεων ASVAB Μαθηματικών 1
Ένα ορθογώνιο κόβεται στη μέση για να δημιουργηθούν δύο τετράγωνα που το καθένα έχει εμβαδόν 25. Ποια είναι η περίμετρος του αρχικού ορθογωνίου;
Ο τύπος για να βρείτε το εμβαδόν ενός τετραγώνου είναι η πλευρά x. Αν κάθε τετράγωνο έχει εμβαδόν 25, τότε οι διαστάσεις του παραλληλογράμμου είναι 5 x 10. Η περίμετρος είναι το άθροισμα όλων των πλευρών και επομένως θα ήταν 5 + 10 + 5 + 10 = 30.
Υπολογίστε το εμβαδόν ενός παραλληλογράμμου με βάση 3 πόδια και ύψος 1,2 πόδια.
Το εμβαδόν ενός παραλληλογράμμου είναι A = bh και το εμβαδόν είναι 1,2 x 3, δηλαδή 3,6 πόδια στο τετράγωνο.
2 − 8 ÷ (24 ÷ 2) =
Θυμηθείτε τη σειρά των εργασιών σας:
- Ολοκληρώστε πρώτα τις λειτουργίες εντός παρενθέσεων.
- Υπολογίστε τους εκθέτες.
- Στη συνέχεια πολλαπλασιάστε και διαιρέστε με τη σειρά από αριστερά προς τα δεξιά.
- Στη συνέχεια προσθέστε και αφαιρέστε με τη σειρά από αριστερά προς τα δεξιά.
2 − 8 ÷ (16 ÷ 2) =
2 − 8 ÷ 8 =
2 − 1 =
1
Ο όγκος αυτού του κουτιού είναι
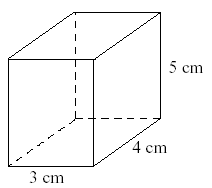
Ο όγκος ενός κυβικού ορθογωνίου είναι μήκος x πλάτος x ύψος: 3 x 4 x 5 = 60
(4x + 2) (x + 1) =
Αυτό είναι ένα πρόβλημα πολλαπλασιαζόμενων διωνύμων. Πολλαπλασιάστε τον πρώτο όρο στο πρώτο δυώνυμο με τους δύο όρους στο δεύτερο δυώνυμο: 4x2 + 4x Στη συνέχεια πολλαπλασιάστε τον δεύτερο όρο στο πρώτο δυώνυμο με κάθε όρο στο δεύτερο δυώνυμο: 2x + 2 Προσθέτοντας τους όλους μαζί παίρνετε: 4x2 + 4x + 2x + 2 4x2 + 6x + 2
Αν 511 = 52 x 5Μ, ποια είναι η αξία του Μ?
Όταν πολλαπλασιάζετε δύο δυνάμεις με την ίδια βάση, μπορείτε πάντα να προσθέσετε τους εκθέτες. Αυτό σημαίνει ότι 11 = 2 + m, άρα m = 9.
Αν (3,2 + 3,3 + 3,5)w = w, τότε ποια είναι η τιμή του w;
Πρώτα αθροίστε τους τρεις αριθμούς που βρίσκονται σε παρένθεση: 10w = w 10w = w θα ισχύει μόνο όταν w = 0.
Ποιο είναι το εμβαδόν αυτού του τραπεζοειδούς;
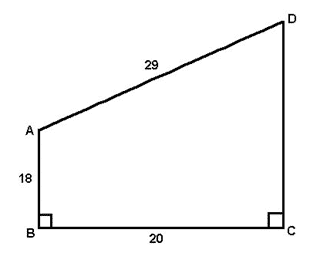
Το τραπεζοειδές αποτελείται από δύο μικρότερα σχήματα: ένα τρίγωνο και ένα ορθογώνιο. Σχεδιάστε μια γραμμή από το σημείο Α σε αυτό το σχήμα για να σχηματίσετε τα δύο σχήματα. Βρείτε το εμβαδόν κάθε σχήματος και μετά προσθέστε τα μαζί για να βρείτε το εμβαδόν του τραπεζοειδούς.
Εμβαδόν ορθογωνίου = μήκος x πλάτος.
Επομένως, το εμβαδόν του ορθογωνίου είναι 18x20 = 360
Εμβαδόν τριγώνου = 1/2(βάση)(ύψος).
Η βάση του τριγώνου είναι 20.
Το ύψος του τριγώνου είναι άγνωστο.
Χρησιμοποιήστε το Πυθαγόρειο Θεώρημα για να βρείτε το ύψος του τριγώνου. ντο2 = α2 + β2 όπου c είναι η υποτείνουσα του τριγώνου.
292 = 202 + (ύψος)2
841 = 400 + (ύψος)2
441 = (ύψος)2
Η τετραγωνική ρίζα του 441 είναι 21
ύψος = 21.
Επομένως, εμβαδόν του τριγώνου = (1/2)(20)(21) = 210. Το συνολικό εμβαδόν του τραπεζοειδούς = 360+210 = 570.
Αν n είναι ένας θετικός ακέραιος διαιρούμενος με το 7, και αν n < 70, ποια είναι η μεγαλύτερη δυνατή τιμή του n;
Εάν γνωρίζετε ένα πολλαπλάσιο ενός αριθμού, μπορείτε να βρείτε τα άλλα πολλαπλάσια προσθέτοντας και αφαιρώντας αυτόν τον αριθμό. Ο αριθμός 70 διαιρείται με το 7. Το μεγαλύτερο πολλαπλάσιο που είναι μικρότερο του 70 θα είναι 70 − 7 = 63.
Ποια από αυτές τις εκφράσεις είναι ισοδύναμη με: 3x3y5 + 3x5y3 − (4x5y3 − 3x3y5)
Το κλειδί σε αυτό το πρόβλημα είναι η διανομή του αρνητικού πρόσημου. Κατά τη διανομή ενός αρνητικού πρόσημου, κάθε όρος έχει μια αλλαγή του πρόσημου από αρνητικό σε θετικό ή από θετικό σε αρνητικό. 3x3y5 + 3x5y3 − (4x5y3 − 3x3y5)
3x3y5 + 3x5y3 − 4x5y3 + 3x3y5
6x3y5 − x5y3
Υπάρχουν δύο φούρνοι πίτσας σε ένα εστιατόριο. Ο φούρνος 1 καίει τρεις φορές περισσότερες πίτσες από τον φούρνο 2. Αν το εστιατόριο είχε συνολικά 12 καμένες πίτσες το Σάββατο, πόσες πίτσες έκαψε ο φούρνος 2;
Ξεκινήστε δημιουργώντας ένα σύστημα εξισώσεων για να αναπαραστήσετε την κατάσταση, αφήνοντας το x να αντιπροσωπεύει τον φούρνο 1 και το y να αντιπροσωπεύει τον φούρνο 2. x = 3y και x + y = 12 Αντικαθιστώντας την πρώτη εξίσωση με τη δεύτερη: 3y + y = 12 άρα y = 3 .
Ένας ανιχνευτής προετοιμάζει το στρατό του για την ετήσια αλιευτική τους αποστολή. Ερευνά κάθε έναν από τους ανιχνευτές του για να ανακαλύψει πόσα καλάμια ψαρέματος έχουν. Ποια είναι η λειτουργία αυτού του συνόλου δεδομένων;
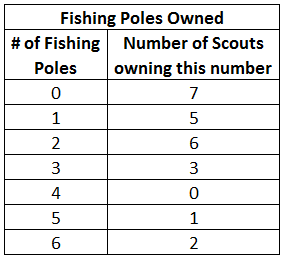
Ο τρόπος λειτουργίας των δεδομένων είναι ο αριθμός που εμφανίζεται πιο συχνά. Σε αυτή την περίπτωση ο μεγαλύτερος αριθμός προσκόπων (7) έχει 0 καλάμια ψαρέματος.
Δεδομένου ενός κύκλου με ακτίνα 0,85 μέτρα, βρείτε το εμβαδόν του κύκλου.
Το εμβαδόν ενός κύκλου είναι ίσο με π r^2. Βάζοντας τις μεταβλητές που γνωρίζουμε, βρίσκουμε το εμβαδόν του κύκλου να είναι 2,27 pi.
3(x − 4) = 18, ποια είναι η τιμή του x;
Ξεκινήστε διαιρώντας και τις δύο πλευρές με το 3 για να ανοίξετε την παρένθεση: x − 4 = 6 Προσθέστε 4 και στις δύο πλευρές για να βρείτε x: x = 10
Ποια είναι η αξία αυτής της έκφρασης:
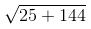
Πρέπει πρώτα να προσθέσετε το 25 και το 144 και μετά να πάρετε την τετραγωνική ρίζα. Η τετραγωνική ρίζα του 169 είναι 13.
Η ευθεία l διέρχεται από το σημείο (−1, 2). Ποιο από τα παρακάτω ΔΕΝ ΜΠΟΡΕΙ να είναι η εξίσωση της ευθείας l;
Η μορφή κλίσης-τομής μιας ευθείας είναι y = mx + b. Εφόσον η γραμμή διέρχεται από το (−1,2), υπάρχουν τρεις πιθανότητες: η γραμμή θα έχει κλίση (το «m» μπροστά από τη μεταβλητή «x»), θα είναι κάθετη (x = −1) ή θα είναι οριζόντια (y = 2). Συνδέστε x = −1 και στις τέσσερις εξισώσεις για να δείτε ποια εξίσωση δεν ικανοποιείται. Η μόνη επιλογή απάντησης που δεν μας δίνει y = 2 είναι (Β)
Αν XY = YZ, και η γωνία Y είναι 90 μοίρες στο παραπάνω σχήμα, ποιο από τα παρακάτω ΔΕΝ ΜΠΟΡΕΙ να συναχθεί;
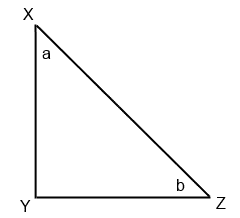
Εδώ ψάχνουμε την επιλογή που ΔΕΝ ισχύει. Εφόσον το τρίγωνο είναι ισοσκελές (XY = YZ), τότε a = b = 45. Αυτό σημαίνει ότι a + b = 90. (A) και (C) πρέπει να είναι αληθές. Για όλα τα ορθογώνια τρίγωνα, ισχύει το Πυθαγόρειο Θεώρημα, άρα ισχύει και το (D). Το (Β) είναι η σωστή απάντηση γιατί δεν είναι αλήθεια ότι XZ < XY. Σε ένα ορθογώνιο τρίγωνο, η υποτείνουσα είναι πάντα η μεγαλύτερη πλευρά.
Ο μέσος όρος του Μπλερ (αριθμητικός μέσος όρος) σε δύο τεστ φυσικής είναι 7. Ποια θα πρέπει να είναι η βαθμολογία του Μπλερ στο επόμενο τεστ για να έχει συνολικό μέσο όρο 8 για όλα τα τεστ;
Ο αριθμητικός μέσος όρος ορίζεται ως το άθροισμα των όρων διαιρούμενο με τον αριθμό των όρων. 7 = άθροισμα / 2 14 = άθροισμα Η προσθήκη της βαθμολογίας του επόμενου τεστ θα αλλάξει τον μέσο όρο σε 8 και οι συνολικοί όροι σε 3. 8 = (14 + νέα βαθμολογία) / 3 24 = 14 + νέα βαθμολογία 10 = νέα βαθμολογία